Next: Trigonometric and Related Up: Irrational and Transcendental Previous: Irrational and Transcendental
Common Lisp the Language, 2nd Edition
![]()
![]()
![]()
![]()
![]()
Next: Trigonometric and
Related Up: Irrational and
Transcendental Previous: Irrational and Transcendental
Along with the usual one-argument and two-argument exponential and
logarithm functions, sqrt is considered to be an
exponential function, because it raises a number to the power 1/2.
[Function]
expnumber
Returns e raised to the power number, where e is the base of the natural logarithms.
[Function]
exptbase-numberpower-number
Returns base-number raised to the power
power-number. If the base-number is of type
rational and the power-number is an
integer, the calculation will be exact and the result will
be of type rational; otherwise a floating-point
approximation may result.

X3J13 voted in March 1989 (COMPLEX-RATIONAL-RESULT) to clarify that
provisions similar to those of the previous paragraph apply to complex
numbers. If the base-number is of type
(complex rational) and the power-number is an
integer, the calculation will also be exact and the result
will be of type (or rational (complex rational)); otherwise
a floating-point or complex floating-point approximation may
result.

When power-number is 0 (a zero of type
integer), then the result is always the value 1 in the type of
base-number, even if the base-number is zero (of any
type). That is:
(expt x 0) == (coerce 1 (type-of x))If the power-number is a zero of any other data type, then the result is also the value 1, in the type of the arguments after the application of the contagion rules, with one exception: it is an error if base-number is zero when the power-number is a zero not of type integer.
Implementations of expt are permitted to use different
algorithms for the cases of a rational power-number and a
floating-point power-number; the motivation is that in many
cases greater accuracy can be achieved for the case of a rational
power-number. For example, (expt pi 16) and
(expt pi 16.0) may yield slightly different results if the
first case is computed by repeated squaring and the second by the use of
logarithms. Similarly, an implementation might choose to compute
(expt x 3/2) as if it had been written
(sqrt (expt x 3)), perhaps producing a more accurate result
than would (expt x 1.5). It is left to the implementor to
determine the best strategies.

X3J13 voted in January 1989 (EXPT-RATIO) to clarify that the preceding
remark is in error, because (sqrt (expt x 3)) does not
produce the same value as (expt x 3/2) in most cases, and
to specify that the specification of the principal value of
expt as given in section 12.5.3 should be regarded as
definitive.
As an example of the difficulty, let 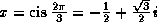 . Then
. Then 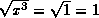 , but
, but 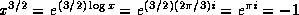 . Another example is
x=-1; then
. Another example is
x=-1; then 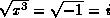 , but
, but 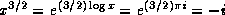 .
.

The result of expt can be a complex number, even when
neither argument is complex, if base-number is negative and
power-number is not an integer. The result is always the
principal complex value. Note that (expt -8 1/3) is not
permitted to return -2; while -2 is indeed one
of the cube roots of -8, it is not the principal cube root,
which is a complex number approximately equal to
#C(1.0 1.73205).

Notice of correction. The first edition gave the incorrect
value #C(0.5 1.73205) for the principal cube root of
-8. The correct value is #C(1.0 1.73205), that
is, 1+SQRT(3)i. I simply don’t know what I was thinking
of!

[Function]
lognumber&optionalbase
Returns the logarithm of number in the base base, which defaults to e, the base of the natural logarithms. For example:
(log 8.0 2) => 3.0
(log 100.0 10) => 2.0The result of (log 8 2) may be either 3 or
3.0, depending on the implementation.
Note that log may return a complex result when given a
non-complex argument if the argument is negative. For example:
(log -1.0) == (complex 0.0 (float pi 0.0))
X3J13 voted in January 1989 (IEEE-ATAN-BRANCH-CUT) to specify certain
floating-point behavior when minus zero is supported. As a part of that
vote it approved a mathematical definition of complex logarithm in terms
of real logarithm, absolute value, arc tangent of two real arguments,
and the phase function as
Logarithm log|z| + i phase zThis specifies the branch cuts precisely whether minus zero is
supported or not; see phase and atan.

[Function]
sqrtnumber
Returns the principal square root of number. If the number is not complex but is negative, then the result will be a complex number. For example:
(sqrt 9.0) => 3.0
(sqrt -9.0) => #c(0.0 3.0)The result of (sqrt 9) may be either 3 or
3.0, depending on the implementation. The result of
(sqrt -9) may be either #c(0 3) or
#c(0.0 3.0).

X3J13 voted in January 1989 (IEEE-ATAN-BRANCH-CUT) to specify certain
floating-point behavior when minus zero is supported. As a part of that
vote it approved a mathematical definition of complex square root in
terms of complex logarithm and exponential functions as
Square root This specifies the branch cuts precisely whether minus zero is
supported or not; see phase and atan.

[Function]
isqrtinteger
Integer square root: the argument must be a non-negative integer, and the result is the greatest integer less than or equal to the exact positive square root of the argument. For example:
(isqrt 9) => 3
(isqrt 12) => 3
(isqrt 300) => 17
(isqrt 325) => 18![]()
![]()
![]()
![]()
![]()
Next: Trigonometric and
Related Up: Irrational and
Transcendental Previous: Irrational and Transcendental
AI.Repository@cs.cmu.edu