Common Lisp the Language, 2nd Edition

Next: Logical Operations on Up: Numbers Previous: Branch CutsPrincipal

12.6. Type Conversions and Component Extractions on Numbers

While most arithmetic functions will operate on any kind of number, coercing types if necessary, the following functions are provided to allow specific conversions of data types to be forced when desired.

[Function]
floatnumber&optionalother

This converts any non-complex number to a floating-point number. With no second argument, if number is already a floating-point number, then number is returned; otherwise a single-float is produced. If the argument other is provided, then it must be a floating-point number, and number is converted to the same format as other. See also coerce.

[Function]
rationalnumber
rationalizenumber

Each of these functions converts any non-complex number to a rational number. If the argument is already rational, it is returned. The two functions differ in their treatment of floating-point numbers.

rational assumes that the floating-point number is completely accurate and returns a rational number mathematically equal to the precise value of the floating-point number.

rationalize assumes that the floating-point number is accurate only to the precision of the floating-point representation and may return any rational number for which the floating-point number is the best available approximation of its format; in doing this it attempts to keep both numerator and denominator small.

It is always the case that

(float (rational x) x) == x

and

(float (rationalize x) x) == x

That is, rationalizing a floating-point number by either method and then converting it back to a floating-point number of the same format produces the original number. What distinguishes the two functions is that rational typically has a simple, inexpensive implementation, whereas rationalize goes to more trouble to produce a result that is more pleasant to view and simpler to compute with for some purposes.

[Function]
numeratorrational
denominatorrational

These functions take a rational number (an integer or ratio) and return as an integer the numerator or denominator of the canonical reduced form of the rational. The numerator of an integer is that integer; the denominator of an integer is 1. Note that

(gcd (numerator x) (denominator x)) => 1

The denominator will always be a strictly positive integer; the numerator may be any integer. For example:

(numerator (/ 8 -6)) => -4 
(denominator (/ 8 -6)) => 3

There is no fix function in Common Lisp because there are several interesting ways to convert non-integral values to integers. These are provided by the functions below, which perform not only type conversion but also some non-trivial calculations as well.

[Function]
floornumber&optionaldivisor
ceilingnumber&optionaldivisor
truncatenumber&optionaldivisor
roundnumber&optionaldivisor

In the simple one-argument case, each of these functions converts its argument number (which must not be complex) to an integer. If the argument is already an integer, it is returned directly. If the argument is a ratio or floating-point number, the functions use different algorithms for the conversion.

floor converts its argument by truncating toward negative infinity; that is, the result is the largest integer that is not larger than the argument.

ceiling converts its argument by truncating toward positive infinity; that is, the result is the smallest integer that is not smaller than the argument.

truncate converts its argument by truncating toward zero; that is, the result is the integer of the same sign as the argument and which has the greatest integral magnitude not greater than that of the argument.

round converts its argument by rounding to the nearest integer; if number is exactly halfway between two integers (that is, of the form integer+0.5), then it is rounded to the one that is even (divisible by 2).

The following table shows what the four functions produce when given various arguments.

Argument    floor       ceiling     truncate    round
----------------------------------------------------------
 2.6          2           3           2           3 
 2.5          2           3           2           2 
 2.4          2           3           2           2 
 0.7          0           1           0           1 
 0.3          0           1           0           0 
-0.3         -1           0           0           0 
-0.7         -1           0           0          -1 
-2.4         -3          -2          -2          -2 
-2.5         -3          -2          -2          -2 
-2.6         -3          -2          -2          -3 
----------------------------------------------------------

If a second argument divisor is supplied, then the result is the appropriate type of rounding or truncation applied to the result of dividing the number by the divisor. For example, (floor 5 2) == (floor (/ 5 2)) but is potentially more efficient.

This statement is not entirely accurate; one should instead say that (values (floor 5 2)) == (values (floor (/ 5 2))), because there is a second value to consider, as discussed below. In other words, the first values returned by the two forms will be the same, but in general the second values will differ. Indeed, we have

(floor 5 2) => 2 and 1 
(floor (/ 5 2)) => 2 and 1/2

for this example.

The divisor may be any non-complex number.

It is generally accepted that it is an error for the divisor to be zero.

The one-argument case is exactly like the two-argument case where the second argument is 1.

In other words, the one-argument case returns an integer and fractional part for the number: (truncate 5.3) => 5.0 and 0.3, for example.

Each of the functions actually returns two values, whether given one or two arguments. The second result is the remainder and may be obtained using multiple-value-bind and related constructs. If any of these functions is given two arguments x and y and produces results q and r, then q y+r=x. The first result q is always an integer. The remainder r is an integer if both arguments are integers, is rational if both arguments are rational, and is floating-point if either argument is floating-point. One consequence is that in the one-argument case the remainder is always a number of the same type as the argument.

When only one argument is given, the two results are exact; the mathematical sum of the two results is always equal to the mathematical value of the argument.

Compatibility note: The names of the functions floor, ceiling, truncate, and round are more accurate than names like fix that have heretofore been used in various Lisp systems. The names used here are compatible with standard mathematical terminology (and with PL/1, as it happens). In Fortran ifix means truncate. Algol 68 provides round and uses entier to mean floor. In MacLisp, fix and ifix both mean floor (one is generic, the other flonum-in/fixnum-out). In Interlisp, fix means truncate. In Lisp Machine Lisp, fix means floor and fixr means round. Standard Lisp provides a fix function but does not specify precisely what it does. The existing usage of the name fix is so confused that it seemed best to avoid it altogether.

The names and definitions given here have recently been adopted by Lisp Machine Lisp, and MacLisp and NIL (New Implementation of Lisp) seem likely to follow suit.

[Function]
modnumberdivisor
remnumberdivisor

mod performs the operation floor on its two arguments and returns the second result of floor as its only result. Similarly, rem performs the operation truncate on its arguments and returns the second result of truncate as its only result.

mod and rem are therefore the usual modulus and remainder functions when applied to two integer arguments. In general, however, the arguments may be integers or floating-point numbers.

(mod 13 4) => 1                 (rem 13 4) => 1 
(mod -13 4) => 3                (rem -13 4) => -1 
(mod 13 -4) => -3               (rem 13 -4) => 1 
(mod -13 -4) => -1              (rem -13 -4) => -1 
(mod 13.4 1) => 0.4             (rem 13.4 1) => 0.4 
(mod -13.4 1) => 0.6            (rem -13.4 1) => -0.4

Compatibility note: The Interlisp function remainder is essentially equivalent to the Common Lisp function rem. The MacLisp function remainder is like rem but accepts only integer arguments.

[Function]
ffloornumber&optionaldivisor
fceilingnumber&optionaldivisor
ftruncatenumber&optionaldivisor
froundnumber&optionaldivisor

These functions are just like floor, ceiling, truncate, and round, except that the result (the first result of two) is always a floating-point number rather than an integer. It is roughly as if ffloor gave its arguments to floor, and then applied float to the first result before passing them both back. In practice, however, ffloor may be implemented much more efficiently. Similar remarks apply to the other three functions. If the first argument is a floating-point number, and the second argument is not a floating-point number of longer format, then the first result will be a floating-point number of the same type as the first argument. For example:

(ffloor -4.7) => -5.0 and 0.3 
(ffloor 3.5d0) => 3.0d0 and 0.5d0

[Function]
decode-floatfloat
scale-floatfloatinteger
float-radixfloat
float-signfloat1&optionalfloat2
float-digitsfloat
float-precisionfloat
integer-decode-floatfloat

The function decode-float takes a floating-point number and returns three values.

The first value is a new floating-point number of the same format representing the significand; the second value is an integer representing the exponent; and the third value is a floating-point number of the same format indicating the sign (-1.0 or 1.0). Let b be the radix for the floating-point representation; then decode-float divides the argument by an integral power of b so as to bring its value between 1/b (inclusive) and 1 (exclusive) and returns the quotient as the first value. If the argument is zero, however, the result is equal to the absolute value of the argument (that is, if there is a negative zero, its significand is considered to be a positive zero).

The second value of decode-float is the integer exponent e to which b must be raised to produce the appropriate power for the division. If the argument is zero, any integer value may be returned, provided that the identity shown below for scale-float holds.

The third value of decode-float is a floating-point number, of the same format as the argument, whose absolute value is 1 and whose sign matches that of the argument.

The function scale-float takes a floating-point number f (not necessarily between 1/b and 1) and an integer k, and returns (*f(expt (floatbf)k)). (The use of scale-float may be much more efficient than using exponentiation and multiplication and avoids intermediate overflow and underflow if the final result is representable.)

Note that

(multiple-value-bind (signif expon sign) 
                     (decode-float f) 
  (scale-float signif expon)) 
== (abs f)

and

(multiple-value-bind (signif expon sign) 
                     (decode-float f) 
  (* (scale-float signif expon) sign)) 
== f

The function float-radix returns (as an integer) the radix b of the floating-point argument.

The function float-sign returns a floating-point number z such that z and float1 have the same sign and also such that z and float2 have the same absolute value. The argument float2 defaults to the value of (float 1float1); (float-sign x) therefore always produces a 1.0 or -1.0 of appropriate format according to the sign of x. (Note that if an implementation has distinct representations for negative zero and positive zero, then (float-sign -0.0) => -1.0.)

The function float-digits returns, as a non-negative integer, the number of radix-b digits used in the representation of its argument (including any implicit digits, such as a ``hidden bit’’). The function float-precision returns, as a non-negative integer, the number of significant radix-b digits present in the argument; if the argument is (a floating-point) zero, then the result is (an integer) zero. For normalized floating-point numbers, the results of float-digits and float-precision will be the same, but the precision will be less than the number of representation digits for a denormalized or zero number.

The function integer-decode-float is similar to decode-float but for its first value returns, as an integer, the significand scaled so as to be an integer. For an argument f, this integer will be strictly less than

(expt b (float-precision f))

but no less than

(expt b (- (float-precision f) 1))

except that if f is zero, then the integer value will be zero.

The second value bears the same relationship to the first value as for decode-float:

(multiple-value-bind (signif expon sign) 
                     (integer-decode-float f) 
  (scale-float (float signif f) expon)) 
== (abs f)

The third value of integer-decode-float will be 1 or -1.

Rationale: These functions allow the writing of machine-independent, or at least machine-parameterized, floating-point software of reasonable efficiency.

[Function]
complexrealpart&optionalimagpart

The arguments must be non-complex numbers; a number is returned that has realpart as its real part and imagpart as its imaginary part, possibly converted according to the rule of floating-point contagion (thus both components will be of the same type). If imagpart is not specified, then (coerce 0 (type-ofrealpart)) is effectively used. Note that if both the realpart and imagpart are rational and the imagpart is zero, then the result is just the realpart because of the rule of canonical representation for complex rationals. It follows that the result of complex is not always a complex number; it may be simply a rational.

[Function]
realpartnumber
imagpartnumber

These return the real and imaginary parts of a complex number. If number is a non-complex number, then realpart returns its argument number and imagpart returns (* 0number), which has the effect that the imaginary part of a rational is 0 and that of a floating-point number is a floating-point zero of the same format.

A clever way to multiply a complex number z by i is to write

(complex (- (imagpart z)) (realpart z))

instead of (*z#c(0 1)). This cleverness is not always gratuitous; it may be of particular importance in the presence of minus zero. For example, if we are using IEEE standard floating-point arithmetic and z=4+0i, the result of the clever expression is -0+4i, a true 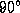rotation of z, whereas the result of (*z#c(0 1)) is likely to be

(4+0i)(+0+i) = ((4)(+0)-(+0)(1))+((4)(1)+(+0)(+0)i
     = ((+0)-(+0))+((4)+(+0))i = +0+4i

which could land on the wrong side of a branch cut, for example.

Next: Logical Operations on Up: Numbers Previous: Branch CutsPrincipal

AI.Repository@cs.cmu.edu